Для построения эпюр напряженно-деформированного состояния

Для построения эпюр напряженно-деформированного состояния рамы формируем систему линейных алгебраических уравнений краевой задачи по МГЭ. Для этого:

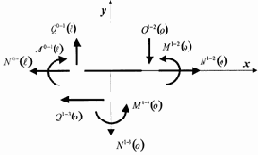
1. Разбиваем раму на 4 стержня. Нумеруем узлы и стрелками обозначаем начало и конец каждого стержня, т. е. формируем орграф расчета рамы (рис. 3.14, а).

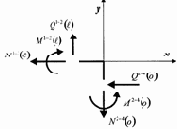
2. Составляем уравнения равновесия и совместности перемещений узлов рамы. Уравнения равновесия узлов 1 и 2 составляем для недеформированного состояния, а уравнения совместности перемещений в соответствии с деформированным состоянием по рис. 3.14, d.

Рис. 3.14, b
Рис. 3.14, c
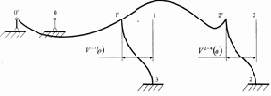
Рис. 3.14, d

 При расчете рамы полагаем, что стержни нерастяжимы и несжимаемы. Составленные уравнения равновесия и совместности перемещений узлов рамы помещаем в матрицу конечных параметров Y

. Матрицы Х* и Y при учете граничных условий примут вид

Х*=	1		; Y=	1		(3.27)
	2			2
	3			3
	4			4
	5			5
	6			6
	7			7
	8			8
	9			9
	10			10
	11			11
	12			12
	13			13
	14			14
	15			15
	16			16
	17			17
	18			18
	19			19
	20			20

Из анализа матрицы Х* следует, что в матрице А* нужно обнулить 1, 3, 5, 6, 7 и 11 столбцы. На место нулевых строк матрицы Х* переносим независимые параметры матрицы Y. Зависимые параметры матрицы Y переносим в матрицу Х* в соответствии с уравнениями их связи. В матрице А* появятся компенсирующие элементы. Разрешающее уравнение задачи статики при

 примет вид

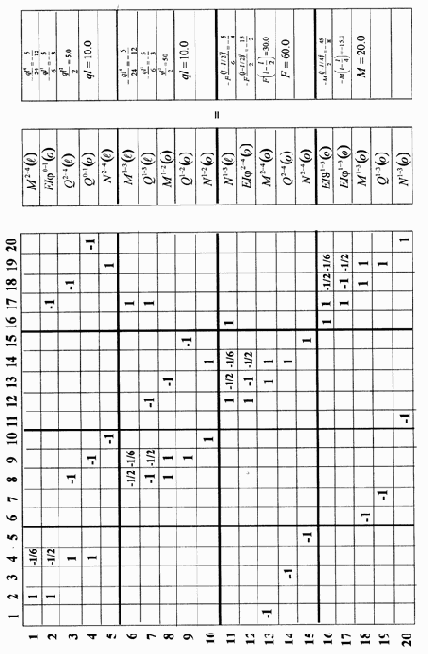(3.28)

<
/p> Программа определения граничных параметров рамы запишется следующим образом (в отдельном файле)

a = zeros (20,20);  b =

zeros (20,1); X = zeros

(20,1);

a(1,2) = 1; a(1,4) = - 1/6; a(2,2) = 1; a(2,4) = - 1/6; a(2,17) = - 1;

a(3,4) = 1; a(3,8) = - 1; a(3,18) = - 1;

a(4,4) = 1; a(4,9) = - 1;

a(4,20) = - 1;

a(5,10) = - 1;

a(5,19) = 1; b(1,1) = - 5/12; b(2,1) = - 5/3; b(3,1) = 5; b(4,1) = 10;

a(6,8) = -1/2;

a(6,9) = -1/6; a(6,17) = 1; a(7,8) = -1; a(7,9) = - 1/2;

a(7,12) = - 1;

a(7,17) = 1; a(8,8) = 1; a(8,9) = 1; a(8,13) = - 1;

a(9,9) = 1; ; a(9,15) = - 1;

a(10,10) = 1; a(10,14) = 1; b(6,1) = - 5/12; b(7,1) = - 5/3;

b(8,1) = 5; b(9,1) = 10;

a(11,12)=1; a(11,13)= -1/2; a(11,14)= -1/6;

a(11,16)=1; a(12,12)=1; a(12,13)=1;

a(12,14)= -1/2;

a(13,1) = -1; a(13,13)=1; a(13,14)=1; a(14,3) = -1; ; a(14,14)=1;

a(15,5)= -1;

a(15,15)= 1; b(11,1) =-5/4;

b(12,1) =-15/2; b(13,1)=30; b(14,1)= 60;

a(16,16)=1; a(16,17)=1; a(16,18)=-1/2;

a(16,19)=-1/6; a(17,17)=1; a(17,18)= -1;

a(17,19)=-1/2;

a(18,6)= -1; a(18,18)=1; a(18,19)=1; a(19,7)= -1; a(19,19)=1;

a(20,11)= -1;

a(20,20)=1; ; b(16,1) =-45/8; b(17,1)= -15; ;

b(18,1)= 20;

X = a

\ b

Значения граничных параметров рамы сведены в таблицу 3.6.


Содержание раздела

---

---