Если сравнить эпюры задачи статики

3.3.7. Определение критических сил рамы

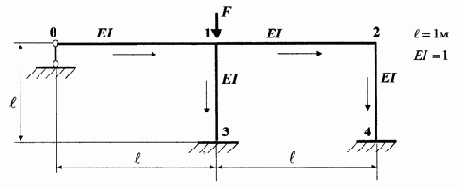Рис. 3.20

Как и для неразрезной балки, определение критических сил потери устойчивости рамы сводится к поиску корней определителя матрицы устойчивости êА*(F) ê= 0, где фундаментальные функции сжатых стержней определяются набором (3.23). Для рамы по рис. 3.20 при потере устойчивости стержень 1-3 испытывает продольно-поперечный изгиб, а другие стержни – статический изгиб. Принимая ориентированный граф расчета, аналогичный задачам статики и динамики (см. рис. 3.14, 3.16), можно существенно облегчить формирование матрицы устойчивости А*(F). Набор компенсирующих элементов остается неизменным, меняются лишь фундаментальные функции стержня 1-3 в сравнении с матрицей задачи статики (3.28). Далее организуется цикл вычисления определителя матрицы устойчивости êА*(F) ê, значения которого и сжимающую силу F выводят в окно команд. При просмотре этих массивов данных легко определить точки, где изменяет знак определитель   d = êА*(F) ê. В этих точках и вычисляются критические силы потери устойчивости данной рамы. При поиске критических сил рекомендуется начинать вычисление определителя матрицы устойчивости с начального значения F0=0.01 EI с шагом DF=0.01 EI. Число вычислений определителя п1=200 – 500 позволяет надежно и достаточно точно определить первую

и последующие критические силы. При решении задачи устойчивости рамы примем, что EI=1,

 м.

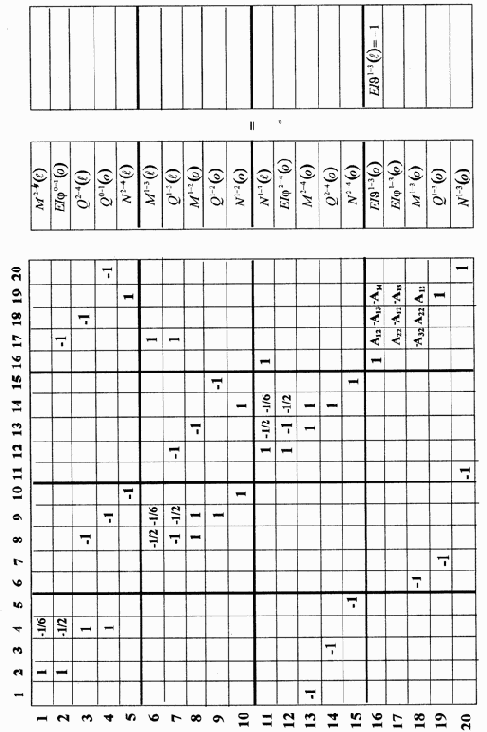
Матрица устойчивости рамы примет вид (см. матрицу А* задачи статики (3.28))

				1		2		3		4		5		6		7		8		9		10		11		12		13		14		15		16		17		18		19		20
		1				1				-1/6
		2				1				-1/2																										-1
		3								1								-1																				-1
		4								1										-1																						-1
		5																				-1																		1
		6																-1/2		-1/6																1
		7																-1		-1/2						-1										1
		8																1		1								-1
A*=		9																		1												-1
10																				1								1														(3.34)
11																								1		-1/2		-1/6				1
		12																								1		-1		-1/2
		13		-1																								1		1
		14						-1																						1
		15										-1																				1
		16																																1		A12		-A13		-A14
		17																																		A22		-A12		-A13
		18												-1																						-A32		A22		A12
		19														-1																								1
		20																						-1																		1

<
/p> Обозначения переменных в программе соответствуют задаче устойчивости неразрезной балки. Программа запишется следующим образом.

n = 20; n1 = 300; f = 0.01; df = 0.1; X = zeros(n1,1); Y= zeros(n1,1);

for m = 1 : n1   n2 = sqrt(f); a = zeros(n,n);

a(1,2)=1; a(1,4)=-1/6; a(2,2)=1; a(2,4)=-1/2; a(2,17)=-1;

a(3,4)=1; a(3,8)=-1; a(3,18)=-1; a(4,4)=1; a(4,9)=-1; a(4,20)=-1;

a(5,10)=-1; a(5,19)=1; a(6,8)=-1/2; a(6,9)=-1/6; a(6,17)=1; a(7,8)=-1;

a(7,9)=-1/2; a(7,12)=-1; a(7,17)=1; a(8,8)=1; a(8,9)=1; a(8,13)=-1;

a(9,9)=1; a(9,15)=-1; a(10,10)=1; a(10,14)=1; a(11,12)=1;

a(11,13)=-1/2; a(11,14)=-1/6; a(11,16)=1; a(12,12)=1; a(12,13)=-1;

a(12,14)=-1/2; a(13,1)=-1; a(13,13)=1; a(13,14)=1; a(14,3)=-1; a(14;14)=1;

a(15,5)=-1; a(15;15)=1; a(16,16)=1; a(16,17)=sin(n2)/n2;

a(16,18)=-(1-cos(n2))/(n2^2); a(16,19)=-(n2-sin(n2))/(n2^3);

a(17,17)=cos(n2); a(17,18)=-a(16,17); a(17,19)=a(16,18);

a(18,6)=-1; a(18,17)=n2*sin(n2); a(18,18)=a(17,17); a(18,19)=a(16,17);

a(19,7)=-1; a(19,19)=1; a(20,11)=-1; a(20,20)=1; d=det(a);

X(m,1)=f; Y(m,1)=d; f=f+df; end;

plot(X,Y); grid on

format long e

[X Y]

Результаты поиска критических сил потери устойчивости рамы



3.3.8. Построение форм потери устойчивости рамы

Для построения форм потери устойчивости рамы необходимо определить граничные параметры рамы при критических силах Fi. Для этого формируется система линейных уравнений краевой задачи по МГЭ, где в правой части в отличие от задачи определения форм собственных колебаний рамы необходимо положить только EIJ 1-3 ()=-1, т.е. b(16,1)=-1. Матричное уравнение данной задачи можно заимствовать из задачи динамики, где необходимо заменить фундаментальные функции поперечных колебаний на фундаментальные функции статического и продольно-поперечного изгибов при граничных значениях координаты х всех стержней (см. (3.35)). Уравнения форм потери устойчивости стержней рамы примут вид (3.12) и (3.26). Программа определения граничных параметров рамы запишется следующим образом:

a=zeros(20,20); b= zeros(20,1); X=zeros(20,1); f=15.098365;



n2=sqrt(f); a(1,2)=1; a(1,4)=-1/6; a(2,2)=1; a(2,4)=-1/2; a(2,17)=-1;

a(3,4)=1; a(3,8)=-1; a(3,18)=-1; a(4,4)=1; a(4,9)=-1; a(4,20)=-1;

a(5,10)=-1; a(5,19)=1; a(6,8)=-1/2; a(6,9)=-1/6; a(6,17)=1; a(7,8)=-1;

(3.35)

a(7,9)=-1/2; a(7,12)=-1; a(7,17)=1; a(8,8)=1; a(8,9)=1; a(8,13)=-1; a(9,9)=1;

a(9,15)=-1; a(10,10)=1; a(10,14)=1; a(11,12)=1; a(11,13)=-1/2; a(11,14)=-1/6;

a(11,16)=1; a(12,12)=1; a(12,13)=-1; a(12,14)=-1/2; a(13,1)=-1; a(13,13)=1; a(13,14)=1;

a(14,3)=-1; a(14,14)=1; a(15,5)=-1; a(15,15)=1; a(16,16)=1;

a(16,17)=sin(n2)/n2; a(16,18)=-(1-cos(n2))/(n2^2);

a(16,19)=-(n2-sin(n2))/(n2^3); a(17,17)=cos(n2); a(17,18)=-a(16,17);

a(17,19)=a(16,18); a(18,6)=-1; a(18,17)=n2*sin(n2); a(18,18)=(17,17);

a(18,19)=a(16,17); a(19,7)=-1; a(19,19)=1; a(20,11)=-1; a(20;20)=1;

b(16,1)=-1; X=a\b; X=X/X(16,1)

Значения относительных граничных параметров сведены в таблицу 3.9.


Содержание раздела

---

---