MATLAB в инженерных и научных расчетах
«Подгонка» кривой

при условии xL £ x £ xU
lsqcurvefit
Принятые обозначения:
• а — скалярный аргумент; х, у — в общем случае векторные аргументы;
• f(а), f(х) — скалярные функции; F(x), c(x), ceq(x), K(x, w) — векторные функции;
• А, Aeq, С, Н — матрицы;
• b, beq, d, f, w, goal, xdata, ydata — векторы;
• xL , xU — соответственно, нижняя и верхняя границы области изменения аргумента.
Применяемые алгоритмы
В рамках пакета Optimization Toolbox все задачи оптимизации делятся на две группы: задачи малой и средней размерности и задачи большой размерности. Соответственно, такое же деление принято для алгоритмов решения данных задач. Разумеется, это не означает, что для решения задач средней размерности нельзя применять алгоритмы большой размерности и наоборот. Просто алгоритмы той или иной группы более эффективны для задач своей размерности.
В пакете Optimization Toolbox реализован широкий набор алгоритмов для решения задач оптимизации средней и малой размерности. Основными для задач без ограничений являются симплексный метод Нелдера—Мида и квазиньютоновские методы. Для решения задач с ограничениями, минимакса, достижения цели и полубесконечной оптимизации использованы алгоритмы квадратичного программирования.
Задачи, сводящиеся к нелинейным МНК, решаются с помощью алгоритмов Ньютона—Рафсона и Левенберга—Марквардта.
Вспомогательные процедуры одномерной (скалярной) оптимизации используют алгоритмы квадратичной (параболической) и кубической интерполяции.
Рассмотрим наиболее часто применяемые в задачах оптимизации функции линейного (linprog) и нелинейного (fmincon) программирования.
1. Функция fmincon
furincon — функция поиска минимума скалярной функции многих переменных при наличии ограничений вида
с(х) £ 0, ceq(x) = 0 ,
А х £ b, Aeq x = beq,
lb < х < ub
- задача нелинейного программирования.
Функция записывается в виде
х = fmincon( fun, x0, A, b)
х = fmincon( fun, x0, A, b, Aeq, beq)
х = fmincon( fun, x0, А, b, Aeq, beq, lb, ub)
х = fmincon( fun, x0, A, b, Aeq, beq, lb, ub, nonlcon)
х = fmincon( fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, options)
х = fmincon( fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, opt1ons, Pl, P2, ...)
[x, fval] = fmincon(...) – возвращается не только оптимальное значение векторного аргумента, но и значение целевой функции в точке минимума fval
;
[x, fval, exitflag] = fmincon(…) – то же, что и предыдущая функция, но возвращается ещё информация о характере завершения вычисления exitflag ;
[x, fval, exitflag, output] = fmincon(…) – то же, что и предыдущая функция, но возвращается ещё информация о результатах оптимизации (выходная структура) output
;
[x, fval, exitflag, output, lambda] = fmincon(...) – то же, что и предыдущая функция, но возвращаются ещё множители Лагранжа lambda
;
[x, fval, exitflag, output, lambda, grad] = fmincon(…) – то же, что и предыдущая функция, но возвращается ещё величина градиента функции в точке минимума grad ;
[x, fval, exitflag, output, lambda, grad, hessian] = fmincon(…) – то же, что и предыдущая функция, но возвращается ещё величина гессиана H функции в точке минимума.
Аргументы функции:
fun — векторная функция векторного аргумента. Должна быть задана либо с помощью функции inline, например:
» fun = inline('sin(x.*x)'):
либо как m -файл, например:
function F = myfun(x)
F = …
nonlcon — функция, возвращающая значения функций-ограничений, а при необходимости (если задано options = optimset('Grad-Constr', 'on')) и их градиентов; должна быть оформлена в виде m-файла, например:
function [c, ceq] = mycon(x)
с = ... % Вычисление левых частей нелинейных неравенств
ceq =... %
Вычисление левых частей нелинейных равенств
function [с, ceq, GC, GCeq] = mycon(x)
с = ... % Вычисление левых частей нелинейных неравенств
ceq = ... % Вычисление левых частей нелинейных равенств
GC = ... %
Градиенты неравенств
GCeq = ... %
Градиенты равенств
* Options – опции ( их можно изменять, используя функцию optimset):
о DerivativeCheck — задает проверку соответствия производных, определенных пользователем, их вычисленным оценкам в виде первых разностей;
o Diagnostics — вывод диагностической информации о минимизируемой функции;
o DiffMaxChange — максимальные значения изменений переменных при определении первых разностей;
о DiffMinChange — минимальные значения изменений переменных при определении первых разностей;
o Display — уровень отображения: 'off' — вывод информации отсутствует, 'iter' — вывод информации о поиске решения на каждой итерации, 'final' — вывод только итоговой информации;
o Goal ExactAchieve — определяет количество целей, которые должны быть достигнуты «точно»;
о GradConstr — использование градиентов для ограничений (опция имеет смысл в случае применения аргумента nonlcon ), возможные значения — 'off и 'on';
o GradObj — использование градиента для целевой функции, определяемого пользователем (возможные значения — 'off и 'on');
о MaxFunEvals — максимальное число вычислений функции;
о Maxlter — максимальное допустимое число итераций;
o MeritFunction — устанавливает вид функции оценки качества достижения цели (возможные значения 'multiobj' или 'singleobj');
o TolCon — допуск останова вычислений при нарушении ограничений;
o TolFun — допуск останова вычислений по величине изменений функции;
o ТоlХ — допуск останова вычислений по величине изменений х;
• exitflag — информация о характере завершения вычислений: если эта величина положительна, то вычисления завершились нахождением решения х, если она равна нулю, то останов произошел в результате выполнения предельного числа итераций, если данная величина отрицательна, то решение не найдено;
• lambda — множители Лагранжа, соответственно, для различных типов ограничений:
o 1ambda. lower — для нижней границы lb;
o 1ambda. upper — для верхней границы ub;
o 1ambda. ineqlin — для линейных неравенств;
o 1ambda. eqlin — для линейных равенств;
o 1ambda. ineqnonlin — для нелинейных неравенств;
o 1ambda. eqnonlin — для нелинейных равенств;
• output — информация о результатах оптимизации:
o output. iterations — число выполненных итераций;
o output. funcCount — число вычислений функции;
o output. algorithm — используемый алгоритм;
o output. cgiterations — число PCG-итераций (только при использовании алгоритма большой размерности);
o output. stepsize — величина конечного шага поиска ( только при использовании алгоритма средней размерности);
o output. firstorderopt — мера оптимальности первого порядка (норма вектора градиента в точке минимума) — только при использовании алгоритма большой размерности)
o LargeScale — может принимать значения 'off' (по умолчанию) и 'on'. В первом слу;чае используется алгоритм средней размерности, во втором — алгоритм большой размерности.
Следующие опции используются только при работе с алгоритмом средней размерности (описание см. выше):
o DerivativeCheck;
o DiffMaxChange;
o DiffMinChange;
o LineSearchType — задание вида алгоритма одномерной оптимизации.
Опции, используемые только в алгоритме большой размерности:
o Hessian — гессиан (в случае матрицы Гессе, задаваемой пользователем, — см. выше);
o HessPattern — задание гессиана как разреженной матрицы (это может привести к существенному ускорению поиска минимума);
o MaxPCGIter — максимальное число итераций PCG-алгоритма (preconditioned conjugate gradient, см. выше);
o PrecondBandWidth — верхняя величина начальных условий для PCG-алгоритма;
o TolPCG — допуск на завершение PCG-итераций;
o TypicalX — типовые величины х;
5) возвращаемая величина output в данном случае имеет дополнительные компоненты:
Пример. Пусть требуется найти минимум функции f(х) = - x1 x2 x3 при начальном значении х = [10; 10; 10] и при наличии ограничений
0 £ x1 + 2 x2 + 2 x3 £ 72.
Решение.
Вначале создадим m-файл, определяющий целевую функцию:
function f = myfun(x)
f =- x(l)*x(2)*x(3) ;
Затем запишем ограничения в виде неравенств:
- x1 - 2 x2 - 2 x3 £ 0
x1
+ 2 x2+ 2 x3
£ 72,
или в матричной форме:
А х £ b,
где

Теперь нахождение решения представляется следующим образом:
»
А = [-1 -2 -2; 1 2 2];
» b = [0; 72];
» x0 = [10; 10; 10]; %
Стартовое значение
» [x, fval] = fmincon('myfun', x0, A, b)
x
=
24.0000
12.0000
12.0000
fval
=
-3.4560e+003
2. Функция linprog
Функция linprog обеспечивает решение задачи линейного программирования.
Функция записывается в виде
х = linprog(f,A,b,Aeq,beq)
х = linprog(f,A,b,Aeq,beq,lb,ub)
х = linprog(f,A,b,Aeq,beq,lb,ub,x0)
х = linprog(f,A,b,Aeq,beq,lb,ub,x0,options)
[x,fval] = linprog(...)
[x,fval,exitflag] = linprog(...)
[x,fval,exitflag,output] = linprog(...)
[x,fval,exitflag,output,lambda] = linprog(...)
Аргументы и возвращаемые величины здесь аналогичны рассмотренным ранее для функции fmincon одним исключением: здесь введен дополнительный аргумент f — вектор коэффициентов линейной целевой функции. Функция может использовать алгоритм большой размерности lipsol или алгоритм средней размерности (метод проекций).
Рассмотрим примеры задач оптимизации.
Пример 1. Требуется найти решение задачи, описывающейся соотношениями
(задача линейного программирования)
f(х) = - 5 x1 – 4 x2 – 6 x3,
х1
- х2 + х3 ? 20 ,
3 x1 + 2 x2 + 4 x3
? 42
3 x1 + 2 x2
? 42
0 ? x1 , 0 ? x2 , 0 ? x3 .
Решение.
>> f = [ -5, -4, -6]; % Вектор коэффициентов линейной целевой функции
>> % Матрица коэффициентов ограничений – неравенств
>> A = [1 -1 1; 3 2 4; 3 2 0];
>> b = [20; 42; 30]; % Вектор ограничений – неравенств
>> % Задание нижних границ переменных (нулей)
>> lb = zeros(3,1);
>> % Поиск решения
>> [x, fval, exitflag, output, lambda] = linprog(f, A, b, [ ], [ ], lb)
Optimization terminated successfully
x =
0.0000
15.0000
3.0000
fval =
-78.0000
exitflag =
1
output =
iterations: 6
cgiterations: 0
algorithm: 'lipsol'
lambda =
ineqlin: [3x1 double]
eqlin [0xl double]
upper [3x1 double]
lower [3x1 double]
Из возвращенной информации, в частности, следует:
• что оптимальное решение х = [0.0000 15.0000 3.0000];
• минимальное значение целевой функции равно -78.0000;
• вычисления завершились нахождением решения (exitflag>0);
• всего было выполнено 6 итераций;
• был использован алгоритм lipsol
Пример 2. Цех малого предприятия должен изготовить 100 изделий трёх типов. Каждого изделия нужно сделать не менее 20 штук. На изделия уходит соответственно 4 , 3,4 и 2 кг металла при его общем запасе 340 кг, а также по 4,75 , 11 и 2 кг пластмассы при её общем запасе 700 кг. Сколько изделий каждого типа х1 , х2 и х3
надо выпустить для получения максимального выпуска в денежном выражении, если цена изделия составляет по калькуляции 40, 30 и 20 грн ?
Данная задача сводится к вычислению максимума функции
f(x1,x2,x3) = 40 x1 + 30 x2 + 20 x3
при наличии ограничений
x1 ? 20, x2
? 20, x3 ? 20
4 x1 + 3,4 x2 + 2 x3
? 340
4,75 x1 + 11 x2 + 2 x3 ? 700
x1 + x2 + x3 = 100
Имеем задачу линейного программирования.
f=[40;30;20];% Вектор коэффициентов линейной целевой функции
% Матрица коэффициентов ограничений – неравенств
A=[4 3.4 2; 4.75 11 2];
b=[340;700]; %вектор ограничений – неравенств
Aeq=[1 1 1]; %матрица коэффициентов ограничений – равенств
beq=[100]; %вектор ограничений – равенств
% Задание нижних границ переменных (нулей)
lb=[20;20;20];
% Поиск решений, определение максимум целевой функции
[x,fval,exitflag,output]=linprog(-f,A,b,Aeq,beq,lb)
Optimization terminated successfully
x =
56.0000
20.0000
24.0000
fval =
-3.3200e+003
exitflag =
1
output =
iterations: 5
cgiterations: 0
algorithm: 'lipsol'
Замечание. Максимизация с помощью функций fminbnd, fminunc, fminsearch, linprog, fmincon, fgoalattain, fminimax, lsqcurvefit и lsqnonlin достигается путём замены целевой функции f(x) на - f(x) ( т. е. изменить знак). Аналогично в задачах квадратичного прогаммирования: там необходимо заменить матрицу Н и вектор f соответственно на - Н и -f .
Пример 3. Оптимальный наклон плоского солнечного коллектора [ 9 ].
Расчёт интенсивности солнечной радиации проводится по следующей формуле [Даффи, Бекма]

где Hb , Hd – прямая и рассеянная составляющие солнечной радиации на
горизонтальной поверхности, Вт ч / м2 ;
(ta) - приведенная поглощательная способность

rd - диффузная отражательная способность. Для системы покрытий из одного, двух,
трёх и четырёх листов стекла rd приблизительно равна 0,16 , 0,24, 0,29, 0,32
соответственно;
a - направленная поглощательная способность поглощающей пластины
a = 0,94 ¸ 0,95 ;
t - пропускательная способность
t
= tr ta ( 3 )
tr - пропускательная способность без учёта поглощения
Для одного покрытия



n1 , n2 - показатели преломления;
q1 , q2 - углы падения и преломления (рис.1).
Если среда 1 воздух, то n1 = 1 , а показатель преломления стекла n2
= 1,526 .
ta - пропускательная способность, учитывающая только поглощение;
ta =

L - толщина стекла, см;
К - коэффициент ослабления стекла, см -1 .
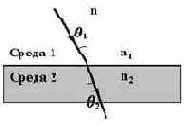
Рис. 1. Преломление луча на границе двух сред