MATLAB в инженерных и научных расчетах
и практически важных случаев связи
|
13 |
  |
14 |
  |
|
15 |
  |
16 |
  |
|
17 |
  |
18 |
  |
|
19 |
  |
20 |
  |
|
21 |
  |
22 |
  |
|
23 |
  |
24 |
  |
|
25 |
  |
26 |
  |
|
27 |
  |
28 |
  |
|
29 |
  |
30 |
  |
2.3. Аппроксимация функций
Одним из распространенных и практически важных случаев связи между аргументом и функцией является задание этой связи в виде некоторой таблицы {xi ; yi}, например, экспериментальные данные. На практике часто приходится использовать табличные данные для приближенного вычисления у при любом значении аргумента х (из некоторой области). Этой цели служит задача о приближении (аппроксимации) функций: данную функцию f(x) требуется приближенно заменить некоторой функцией g(х) так, чтобы отклонение g(х) от f(x) в заданной области было наименьшим. Функция g(х) при этом называется аппроксимирующей. Если приближение строится на заданном дискретном множестве точек {xi}, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и др. При построении приближения на непрерывном множестве точек (например, на отрезке [a, b]) аппроксимация называется непрерывной или интегральной. MATLAB имеет мощные средства точечной и непрерывной аппроксимации с визуализацией результата. Рассмотрим наиболее важную точечную аппроксимацию (обработка экспериментальных данных).
Пример 4. Используя линейную и полиномиальную аппроксимации, получить эмпирические формулы для функции у=f(x), заданной в табличном виде:
|
xi |
0.75 |
1.50 |
2.25 |
3.00 |
3.75 |
|
yi |
2.50 |
1.20 |
1.12 |
2.25 |
4.28 |
Протокол программы. В окне команд набираются значения xi и yi. Далее выполняется команда построения графика только узловых точек.
>> x
= [0.75, 1.50, 2.25, 3.00, 3.75] ;
>> y
= [2.50, 1.20, 1.12, 2.25, 4.28] ;
>> рlot (x, y, ¢ 0 ¢) ;
Появляется окно с символами ¢ 0 ¢ на месте узловых точек (рис. 2.1).
 |
|||||||||
|
4 |
|||||||||
|
3.5 |
|||||||||
  |
|||||||||
|
2.5 |
|||||||||
 |
|||||||||
 |
|||||||||
|
1 |
|||||||||
|
0.5 |
|||||||||
|
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
Внимание. Следует помнить, что при полиномиальной аппроксимации максимальная степень полиноме на 1 меньше
числа экспериментальных точек!
На панели инструментов окна графика узловых точек в меню Tools исполняем команду Basic Fitting. Появляется окно Основной Монтаж. В этом окне птичкой отмечаются необходимые данные аппроксимации. В частности, можно задать следующие операции:
- показать уравнение аппроксимирующей функции у = g(х);
- выбрать метод подбора: сплайн интерполяции
эрмитовская интерполяция
линейный
квадратные
кубический
…………….
В нашей задаче выбираем линейную и полиномиальную аппроксимации. В окне графика появляются соответствующие графики разноцветом и формулы аппроксимирующих функций (рис. 2.2).
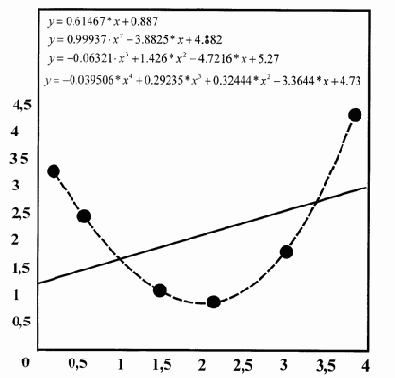 |
Чтобы узнать погрешность аппроксимации, надо отметить птичкой параметр График остатка в окне Основной Монтаж, и Показать норму остатков. График погрешностей с нормами можно вынести в отдельное окно, или вместе с графиком и аппроксимирующих функций – суб-график. Норма погрешностей указывает на статистическую оценку среднеквадратической погрешности. Чем она меньше, тем точнее полученная аппроксимирующая функция у = g(х). В нашем примере:
Linear : norm of residuals (норма погрешности) = 2.1061
Quadratic : norm of residuals = 0.10736
Cubic : norm of residuals = 0.035857
4 th degree : norm of residuals = 9.6305e-015.
График погрешностей можно выводить в виде диаграмм (зоны), линий (линии) или отдельных точек (фрагменты). Сам график погрешностей представляет собой зависимость разности g(х) - f(x) в условных точках, соединенных прямыми линиями.