MATLAB в инженерных и научных расчетах
Символьные операции математического анализа
1. Функция вычисления производных – diff
Для вычисления в символьном виде производных от выражения S служит функция diff, записываемая в формате diff(S,'v') или diff(S, sym('v')) Она возвращает символьное значение первой производной от символьного выражения или массива символьных выражений S по переменной v. Эта функция возвращает

• diff(S, n) — возвращает п-ю (п — целое число) производную символьного выражения или массива символьных выражений S по переменной v.
• diff(S, V, n) и diff(S, n, V) – возвращает п-ю производную S по переменной v.
Примеры:
» x =sym( 'x' ); y=sym( 'у' );
» diff(x^y)
ans =
х^у*y / x
» slmplify(ans)
ans =
x^(y-1)*y
» diff(s1n(y*x), x, 3)
ans =
- cos(y*x)*y^3
» diff([x^3 sin(x) exp(x)], x)
ans =
[ 3*x^2, cos(x), exp(x)]
2. Функция интегрирования – int
Функция int вычисляет неопределенные и определенные интегралы
• int(S) — возвращает символьное значение неопределенного интеграла от символьного выражения или массива символьных выражений S по переменной, которая автоматически определяется функцией findsym. Если S — скаляр или матрица, то вычисляется интеграл по переменной 'х'.
• int(S, v) — возвращает неопределенный интеграл от S по переменной v .
• int(S, a, b) — возвращает определенный интеграл от S с пределами интегрирования от а до b, причем пределы интегрирования могут быть как символьными, так и числовыми.
• int(S, v, a, b) — возвращает определенный интеграл от S по переменной v с пределами от а до b.
Примеры:
» int(sin(x)^3, x)
ans =
- l/3*sin(x)^2*cos(x)-2/3*cos(x)
» int(log(2*x), x)
ans =
log(2*x)*x - x
» int((x^2-2)/(x*3-l), x, l, 2)
ans =
-inf
» int((x^2-2)/(x*3-l), x, 2, 5)
ans =
- 2/3*1og(2) + 2/3*1og(31) + 2/3*3^(l/2)*atan(11/3*3^(l/2)) -...
2/3*log(7) - 2/3*3^(1/2)*atan(5/3*3^(l/2))
• solve(expr1, expr2,... exprN, var1, var2,... varN) — возвращает значения переменных var1, при которых соблюдаются равенства, заданные выражениями exprI. Если в выражениях не используются знаки равенства, то полагается ехргI
= 0;
• solve(expr1, expr2, ..... exprN) — аналогична предшествующей функции, но переменные, по которым ищется решение, определяются функцией findsym.
Примеры решения уравнений:
» syms x у;
» so1ve(x^3 -1, x)
ans =
[ 1]
[ -1/2+1/2*i*3^(1/2)]
[ -1/2-1/2*i*3^(1/2)]
» syms a b с
» solve(a*x^2+b*x+c)
ans =
[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))]
[ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]
»S = solve(‘x+y=3’, ‘x*y^2=4’, x, y)
S =
x : [ 3x1 sym ]
y : [ 3x1 sym ]
» S.x
ans =
[4]
[1]
[1]
» S.y
ans =
[-1]
[2]
[2]
» solve(‘sin(x)=0.5’, x)
ans =
0.52359877559829887307710723054658
7. Решение дифференциальных уравнений – dsolve
Для решения дифференциальных уравнений в форме Коши MATLAB имеет следующую функцию:
• dsolve( 'eqn1', 'eqn2', ...) — возвращает аналитическое решение системы дифференциальных уравнений с начальными условиями. Они задаются равенствами eqnl
(вначале задаются уравнения, затем начальные условия).
По умолчанию независимой переменной считается переменная 't', обычно обозначающая время. Можно использовать и другую переменную, добавив ее в конец списка параметров функции dsolve. Символ D обозначает производную по независимой переменной, то есть d / dt, при этом D2 означает d2 / dt2 и т. д. Имя независимой переменной не должно начинаться с буквы D.
Начальные условия задаются в виде равенств 'у(а)=b' или 'Dy(a)=b', где у — независимая переменная, а и b — константы. Если число начальных условий меньше, чем число дифференциальных уравнений, то в решении будут присутствовать произвольные постоянные С1, С2 и т. д.
Примеры применения функции dsolve:
» dsolve('D2x = -2*x')
ans =
Cl*cos(2^(1/2)*t) + C2*sin(2^(l/2)*t)
» dsolve('D2y = -2*x + y', 'у(0) = 1 , 'х')
ans =
(2*х*ехр(х) + (- С2 + 1)*ехр(х)^2 + С2 / ехр(х)
Графические возможности Simbolic
1. Графопостроитель – funtool
Команда funtool
создает интерактивный графический калькулятор, позволяющий быстро построить две функции одной переменной - f(x) и g(x). Например, одна может задавать собственно функцию, а другая — ее производную. Функции обозначаются как ' f = ' и ' g = ' и после знака равенства можно набрать функции с помощью клавиш калькулятора в его нижней части. С помощью полей 'х = ' и ' а = ' можно задать диапазон изменения переменной х и значение масштабирующего параметра а.
При запуске команды funtool появляются окна для двух функций и окно калькулятора (рис. 4.1). По умолчанию заданы функции f(x)
= х и g(x) = 1, предел изменения х от -2? до 2? и а = 1/2.
Верхний ряд кнопок вычислителя относится только к функции f(x) и задает следующие операторы:
• df/dx — символьное дифференцирование f(x);
• int f
— символьное интегрирование f(x) при наличии замкнутой формы;
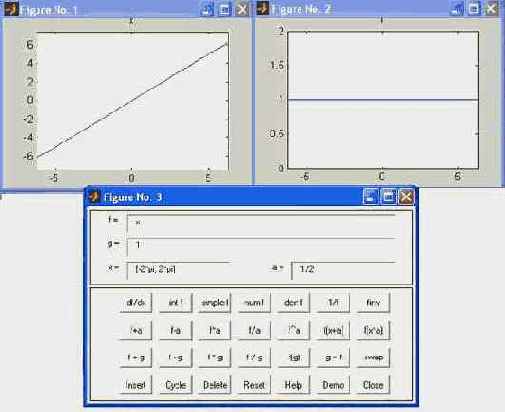
Рис. 4.1. Внешний вид графопостроителя funtool
• simple f — упрощение выражения, если таковое возможно;
• num f — выделение числителя рационального выражения;
• den f — выделение знаменателя рационального выражения;
• 1/f — замена f(x) на 1 / f(x);
• finv — замена f(x) инверсной функцией.
Второй ряд клавиш выполняет операции масштабирования и сдвига f(x) с применением параметра 'а'.
Третий ряд клавиш предназначен для осуществления бинарных операций над функциями f(x) и g(x).
Четвертый ряд клавиш служит для работы с памятью калькулятор и иных операций:
• Insert — помещает текущую функцию в список функций.
• Cycle — выполняет текущую функцию из списка.
• Delete — удаляет выделенную функцию из списка.
• Reset — устанавливает f, g, x, а и fxl i st в исходное состояние.
• Help — выводит описание калькулятора.
• Demo — запускает демонстрационный пример.
• Close — завершает работу с калькулятором.
Благодаря описанным средствам вычислитель позволяет задать инересующую вас функцию, выполнить ее преобразования (например, дифференцирование и интегрирование) и, наконец, построить график функции и результатов ее преобразования (рис.4.2)
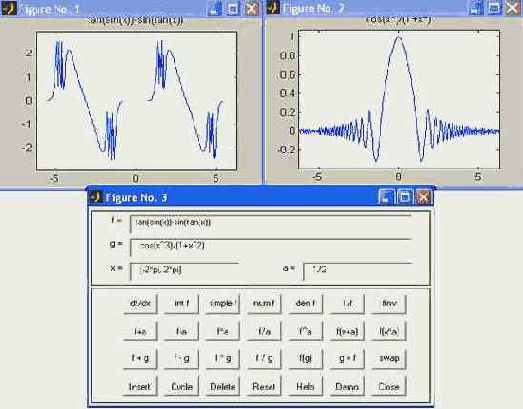
Рис. 4.2. Построения графиков некоторых функций
Таким образом, графопостроитель funtool является весьма удобным средством визуализации графиков самых различных функций.
2. Графики поверхностей – ezsurf и ezsurfc
Команда ezsurf служит для построения графиков поверхностей, задаваемых функциями двух переменных f(x, у):
• ezsurf(f) — построение поверхности f(x,y) с параметрами х и у, меняющимися по умолчанию от -2? до 2?;
• ezsurf(f,domain) — построение поверхностиf(x,y) с пределами изменения х и у, заданными параметром domain;
• ezsurf(x,y,z) — построение поверхности, заданной параметрически зависимостями x(s, t), y(s, t), z(s, t) при s и t, меняющихся в интервале от -2? до 2?;
• ezsurf(x,y,z,[smin, smax, tmin, tmax]) — построение поверхности, заданной параметрически зависимостями x(s, t), y(s, t), z(s, t) при s
и t
меняющихся в заданном интервале.
Следующий пример показывает действие этой команды:
» syms x у
» ezsurf(rea1(asec(x+i*y)))
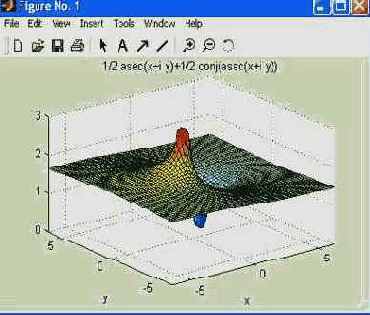
Рис. 4.3. Пример построения графика поверхности командой ezsurf
Аналогичная по синтаксису записи группа команд ezsurfc строит еще и контурный график поверхности на плоскости, лежащей под поверхностью.
Применение средств символьных вычислений в
теоретической механике
1. Решение задач статики.
При решении некоторых прикладных задач оптимизации желательно получать аналитические решения, устанавливающие функциональную связь между заданными параметрами и величинами, подлежащими определению. В этом случае целевая функция оптимизации имеет явное выражение и её максимум (минимум) определяется обычными методами математического анализа. Рассмотрим следующую задачу о равновесии конструкции:
З а д а н и е С 1. Определение наибольшего значения реакции опоры для
составной конструкции
На плоскую конструкцию, состоящую из двух невесомых элементов, которые в точке С соединены шарниром, наложены следующие связи:
1) Шарнирная опора на катках в точке А ;
2) Неподвижный цилиндрический шарнир в точке D ;
3) Горизонтальный невесомый стержень в точке К.
На конструкцию действуют:
1. Пара сил с моментом М = 5 кН м ( в точке Е).
2. Две сосредоточенные силы F1 = 4 кН ( в точке D ) и F2 = 6 кН ( в точке А ), образующие в точке приложения с контуром элемента соответственно углы ? и 300
.
3. Перпендикулярно к действующему участку ( участок АВ
) равномерно распределённая нагрузка интенсивности q = 10 кН / м.
Длина каждого участка конструкции а = 0,4 м. Предполагая, что конструкция находится в равновесии, найти при каком значении угла наклона ? силы F1 реакция шарнира D (

Решение. Для определения искомых реакций можно поступить двояко, либо мысленно расчленить систему тел (составную конструкцию) на отдельные твёрдые тела и рассмотреть равновесие каждого из тел в отдельности, либо, применяя принцип затвердевания, вначале рассмотреть равновесие всей конструкции, а затем равновесие её отдельных элементов.
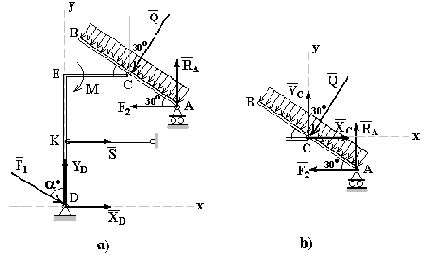
Рис. 4.4. Схема составной конструкции
I. Прежде рассмотрим равновесие всей конструкции.
1. Объект равновесия – составная конструкция.
2. Связи – шарнирная опора на катках в точке А, неподвижный цилиндрический шарнир в точке D и невесомый стержень в точке К . На конструкцию действуют сосредоточенные силы F1 и F2 , равномерно распределённая нагрузка интенсивности q и пара сил с моментом М.
3. Действие связей заменим их реакциями RA , ХD , УD
, S . Равномерно распределённую нагрузку заменим равнодействующей
Q = q 2 a = 8 kH.
Другие активные силы - F1 , F2 и пара сил с моментом М.
4. Составим уравнения равновесия ( система координат Dху изображена на ри-
сунке 4.5a)

- F2 + F1 sin ? – Q cos 600
+ S = 0


+ RА a cos 300 + S a + XD 2 a = 0.
Данная система уравнений содержит четыре неизвестных XD , УD , S , RA .
II. Рассмотрим теперь равновесие правой части конструкции ( Рис. 4.5b ).
1. Объект равновесия – правая часть конструкции.
2. Связи – шарнирная опора на катках в точке А и соединительный шарнир С. На объект равновесия действует сосредоточенная сила F2 , равнодействующая распределённой нагрузки Q и реакции связей XC , УC , RA .
3. Составим уравнения равновесия ( в системе координат Cху )


+ YC - Q cos 300 = 0 ( б )

Решаем систему шести уравнений (а) – (б) с шестью неизвестными, система (б) является независимой и содержит три неизвестных. Находим, из третьего уравнения
RA = F2 tg 300 = 6 tg 300 = 3,464 кН ,
из первого – XC = F2 + Q sin 300 = 10 кН,
из второго уравнения УС = Q cos 300 – RA = 3,464 кН.
Решаем систему уравнений (а), для этого воспользуемся символьными вычислениями системы MATLAB
syms XD YD S al %символьные переменные
Q1=solve('XD-6+4*sin(al)-8*0.5+S=0','YD-8*0.866+3.464-4*cos(al)=0',...
'-6*0.5*0.4+4*0.4*cos(al)+4*2*0.4*sin(al)-5-YD*0.4+3.464*0.4*0.866+S*0.4+XD*2*0.4=0'...
,XD,YD,S); %решение уравнений равновесия
digits(6) %количество значащих цифр
S=vpa(Q1.S); %величина реакции S
XD=vpa(Q1.XD); %величина реакции XD
YD=vpa(Q1.YD); %величина реакции YD
RD=sqrt(XD^2+YD^2) %величина полной реакции шарнира D
ezplot(RD,-pi/2,pi) %график функции RD=RD(al)
solve(diff(RD,al),al) %нахождение экстремума
S =
1.03583
XD =
5.96418 – 4.*sin(al)
YD =
3.46400 + 4.*cos(al)
RD =
((5.96418 – 4.*sin(al))^2 + (3.46400 + 4.*cos(al))^2)^(1/2)
ans =
[ 2.09698 ]
[ - 1.04461 ]
Таким образом, наибольшее значение полная реакция RD шарнира D имеет при ? = - 1,04461 , а наименьшее – при ? = 2,09698.
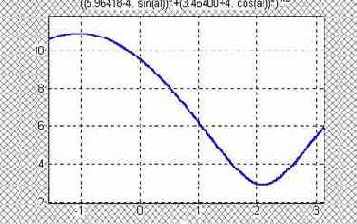
Рис. 4.5. График зависимости RD =

Реакции связей RA , XC , YC , S не зависят от угла величины ?
RA = 3,464 кН , XC = 10 кН , YC = 3,464 кН , S = 4,03583 кН,
а наибольшее и наименьшее значения полной реакции шарнира D соответственно равны :
RDmin = 2,89717 кН при ? = 2,09698,
RDmax = 10,989715 кН при ? = - 1,04461.
Варианты задания. Конструкция состоит из двух частей. Установить, при каком значении угла ? для силы F1 реакция опоры А (

Необходимые для расчёта данные приведены в таблице 4.1
Таблица 4.1
|
Номер варианта |
Р1 |
Р2 |
М, кН м |
q, кН/м |
Номер варианта |
Р1 |
Р2 |
М, кН м |
q, кН/м |
|
кН |
кН |
||||||||
|
1 |
5,0 |
- |
24,0 |
0,8 |
16 |
7,0 |
10,0 |
14,0 |
3,8 |
|
2 |
6,0 |
10,0 |
22,0 |
1,0 |
17 |
9,0 |
12,0 |
26,0 |
4,0 |
|
3 |
7,0 |
9,0 |
20,0 |
1,2 |
18 |
11,0 |
10,0 |
18,0 |
3,5 |
|
4 |
8,0 |
- |
18,0 |
1,4 |
19 |
13,0 |
9,0 |
30,0 |
3,0 |
|
5 |
9,0 |
- |
16,0 |
1,6 |
20 |
15,0 |
8,0 |
25,0 |
2,5 |
|
6 |
10,0 |
8,0 |
25,0 |
1,8 |
21 |
10,0 |
7,0 |
20,0 |
2,0 |
|
7 |
11,0 |
7,0 |
20,0 |
2,0 |
22 |
5,0 |
6,0 |
15,0 |
1,5 |
|
8 |
12,0 |
6,0 |
15,0 |
23 |
8,0 |
5,0 |
10,0 |
1,4 |
|
|
9 |
13,0 |
- |
10,0 |
24 |
11,0 |
4,0 |
5,0 |
1,3 |
|
|
10 |
14,0 |
- |
12,0 |
25 |
14,0 |
6,0 |
7,0 |
1,2 |
|
|
11 |
15,0 |
5,0 |
14,0 |
26 |
12,0 |
8,0 |
9,0 |
1,1 |
|
|
12 |
12,0 |
4,0 |
16,0 |
27 |
10,0 |
7,0 |
11,0 |
1,0 |
|
|
13 |
9,0 |
6,0 |
18,0 |
28 |
8,0 |
9,0 |
13,0 |
1,2 |
|
|
14 |
6,0 |
- |
20,0 |
29 |
6,0 |
10,0 |
15,0 |
1,4 |
|
|
15 |
5,0 |
8,0 |
22,0 |
30 |
10,0 |
12,0 |
17,0 |
1,6 |
/p> Схемы конструкций для каждого из вариантов приведены на рисунках 4.6 – 4.8
2. Решение задач кинематики точки.
З а д а н и е К1. Определение скорости и ускорения точки по заданным
уравнениям её движения
По заданным уравнениям движения точки М x = x
( t ) y = y
( t ) установить вид её траектории и для момента времени t
= t1
( c ) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорение, а также радиус кривизны траектории.
Необходимые для решения данные приведены в таблице 4.2.
Пример выполнения задания К1. Движение точки на плоскости Оху определяется уравнениями

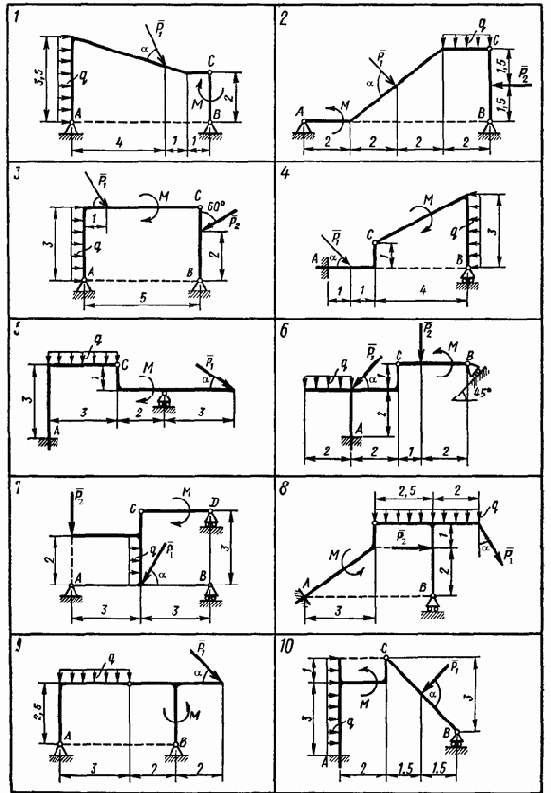
Рис. 4.6
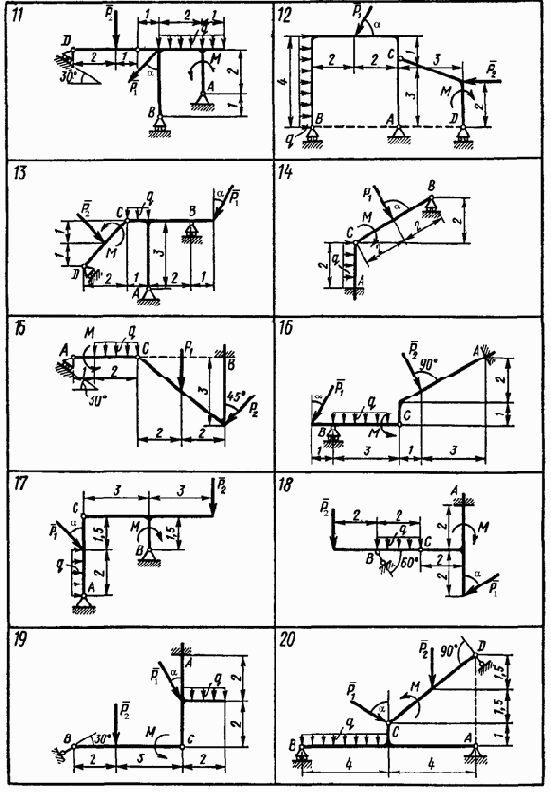
Рис. 4.7
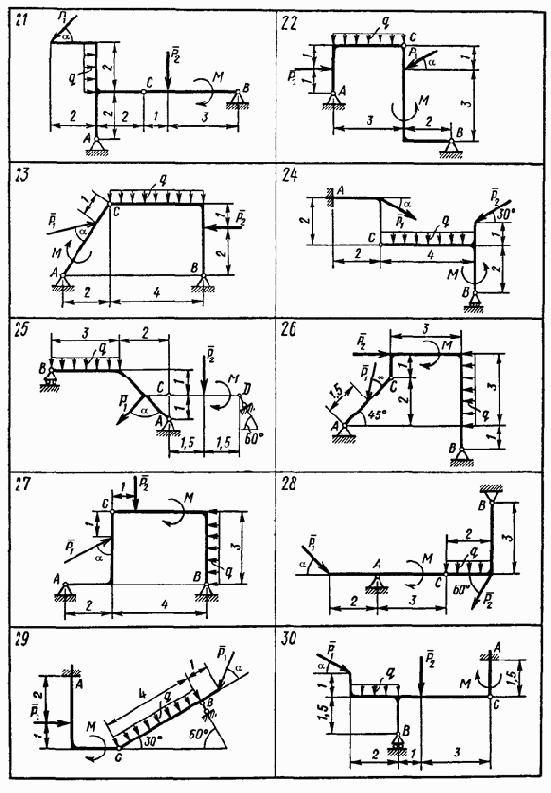
Рис. 4.8
Задан момент времени t1
= 0 .
Необходимо:
1. Определить уравнение траектории точки.
2. Построить траекторию и указать на траектории положение точки в заданный
момент времени t1
.
3. Для заданного момента времени найти скорость и ускорение
точки, её тангенциальное и нормальное ускорения, значение радиуса кривизны траектории.
4. Векторы скорости и ускорения точки показать на траектории.
Решение.
1. Движение точки задано координатным способом.
Для определения уравнения траектории точки, соответствующей заданным уравнениям
движения, исключаем
время t . Из уравнений
движения имеем
cos2 t2 = x2 / 16 , sin2 t2 = y2 .
Применяя основное тригонометрическое тождество, получим

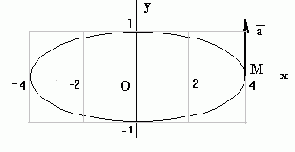
Таким образом, траекторией точки является эллипс.
2. Определяем скорость точки
Vx =


V =


при t1
= 0 c : Vx = 0 и Vy = 0
V =

При малых значениях t ( 0 < t << 1) скорость определяется выражениями:
Vx = - 8 t3 , Vy = 2 t , V =

3. Определяем ускорение точки
ax =

при t1 = 0 c ax
= 0 м / с2 , аy = 2 м / с2 ,
a =

При малых значениях t ( 0 < t << 1) ускорение представляется в виде:
ax
= - 8 t2 - 16 t2 = - 24 t2 , ay
= 2 - 4 t3 , a =

4. По формулам



находим тангенциальное и нормальное ускорения точки в момент t1 ® 0 с ,






при t = 0 an = 0 м / с2 .
5. По формуле


 |