Машины Тьюринга

Формально машина Тьюринга (Tm) - это

$Машины Тьюринга$

, где

Q - конечное множество состояний;

$Машины Тьюринга$

- множество заключительных состояний;

$Машины Тьюринга$

- множество допустимых ленточных символов; один из них, обычно обозначаемый B, - пустой символ

$Машины Тьюринга$

- множество входных символов, подмножество \Gamma, не включающее B,

D функция переходов, отображение из

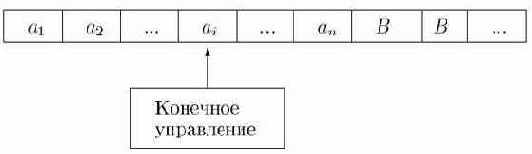
$Машины Тьюринга$

для некоторых аргументов функция D может быть не определена.

$Машины Тьюринга$

- начальное состояние.

Рис. 2.2. Машина Тьюринга

Так определенная машина Тьюринга называется детерминированной. Недетерминированная машина Тьюринга для каждой пары

$Машины Тьюринга$

может иметь несколько возможных переходов. В начале n ячеек ленты содержат вход

$Машины Тьюринга$

, остальная часть ленты содержит пустые символы. Обозначим конфигурацию машины Тьюринга как

$Машины Тьюринга$

, где

$Машины Тьюринга$

- текущее состояние, i - выделенный элемент строки, "положение головки" , w - текущее содержимое занятого участка ленты. Если головка сдвигается с ячейки, машина должна записать в нее символ, так что лента всегда состоит из участка, состоящего из конечного числа непустых символов и бесконечного количества пустых символов.

Шаг Tm определим следующим образом.

Пусть (q, A1, A2, ... An, i) - конфигурация Tm,

где

$Машины Тьюринга$

Если

$Машины Тьюринга$

и D(q, Ai) = (p, A, R)

(R от англ. Right), то

$Машины Тьюринга$

и)

$Машины Тьюринга$

То есть Tm печатает символ A и передвигается вправо.

Если

$Машины Тьюринга$

(L от англ. Left), то если i = n, то допустимо A = B и

$Машины Тьюринга$

Tm печатает A и передвигается влево, но не за конец ленты.

Если i = n + 1, головка просматривает пустой символ B.

Если D(q, B) = (p, A, R), то

$Машины Тьюринга$

Если D(q, B) = (p, A, L), то допустимо A=B и

$Машины Тьюринга$

Если две конфигурации связаны отношением

$Машины Тьюринга$

, то мы говорим, что вторая получается из первой за один шаг. Если вторая получается из первой за конечное, включая ноль, число шагов, то такое отношение будем обозначать

$Машины Тьюринга$

Язык, допускаемый Tm, это множество таких слов из T*, которые будучи расположены в левом конце ленты переводят Tm из начального состояния q0 с начальным положением головки в самом левом конце ленты в конечное состояние. Формально, язык, допускаемй Tm, это

$Машины Тьюринга$

Если Tm распознает L, то Tm останавливается, то есть не имеет переходов после того, как слово допущено. Однако, если слово не допущено, возможно, что Tm не останавливается.

Язык, допускаемый некоторой Tm, называется рекурсивно перечислимым. Если Tm останавливается на всех входах, то говорят, что Tm задает алгоритм и язык называется рекурсивным.

Существует машина Тьюринга, которая по некоторому описанию произвольной Tm и кодированию слова x моделирует поведение Tm со входом x. Такая машина Тьюринга называется универсальной машиной Тьюринга.

Содержание раздела

Главная сайта