Теория и реализация языков программирования
Связь регулярных множеств, конечных автоматов и регулярных грамматик
В разделе 3.3.3 приведен алгоритм построения детерминированного конечного автомата по регулярному выражению. Рассмотрим теперь как по описанию конечного автомата построить регулярное множество, совпадающее с языком, допускаемым конечным автоматом.
Теорема 3.1. Язык, допускаемый детерминированным конечным автоматом, является регулярным множеством.
Доказательство. Пусть L - язык, допускаемый детерминированным конечным автоматом

Введем De - расширенную функцию переходов автомата M: De(q, w) = p, где


Обозначим посредством


Иными словами,



Таким образом, определение

- Цепочка w принадлежит , то есть при анализе цепочки w автомат никогда не достигает состояний с номерами, большими или равными k.

- Цепочка w может быть представлена как w = w1w2w3, где (подцепочка w1 переводит M сначала в qk),
 (подцепочка w2 переводит M из qk обратно в qk, не проходя через состояния с номерами, большими или равными k), и
(подцепочка w2 переводит M из qk обратно в qk, не проходя через состояния с номерами, большими или равными k), и (подцепочка w3 переводит M из состояния qk в qj) - рис. 3.16.
(подцепочка w3 переводит M из состояния qk в qj) - рис. 3.16.
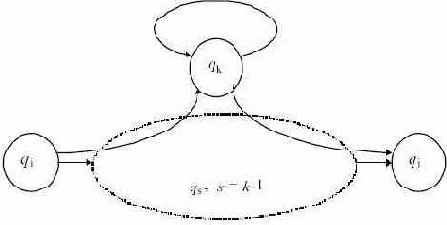
Рис. 3.16.
Тогда

Таким образом, для всякого регулярного множества имеется конечный автомат, допускающий в точности это регулярное множество, и наоборот - язык, допускаемый конечным автоматом есть регулярное множество.
Рассмотрим теперь соотношение между языками, порождаемыми праволинейными грамматиками и допускаемыми конечными автоматами.
Праволинейная грамматика G = (N, T, P, S) называется регулярной, если
(1) каждое ее правило, кроме S




(2) в том случае, когда

Лемма. Пусть G - праволинейная грамматика. Существует регулярная грамматика G' такая, что L(G) = L(G').
Доказательство. Предоставляется читателю в качестве упражнения.
Теорема 3.2. Пусть G = (N, T, P, S) - праволинейная грамматика. Тогда существует конечный автомат M = (Q, T, D, q0, F) для которого L(M) = L(G).
Доказательство. На основании приведенной выше леммы, без ограничения общности можно считать, что G - регулярная грамматика.
Построим НКА M следующим образом:
- состояниями M будут нетерминалы G плюс новое состояние R, не принадлежащее N. Так что ,

- в качестве начального состояния M примем S, то есть q0 = S,
- если P содержит правило S e, то
 , иначе F = {R}. Напомним, что S не встречается в правых частях правил, если
, иначе F = {R}. Напомним, что S не встречается в правых частях правил, если ,
,
- состояние , если
 . Кроме того, D(A, a) содержит все B такие, что
. Кроме того, D(A, a) содержит все B такие, что , для каждого
, для каждого .
.
M, читая вход w, моделирует вывод w в грамматике G. Покажем, что L(M) = L(G). Пусть






Аналогично, если







Теорема 3.3. Для каждого конечного автомата M = (Q, T, D, q0, F) существует праволинейная грамматика G = (N, T, P, S) такая, что L(G) = L(M).
Доказательство. Без потери общности можно считать, что автомат M - детерминированный. Определим грамматику G следующим образом:
- нетерминалами грамматики G будут состояния автомата M. Так что N = Q,
- в качестве начального символа грамматики G примем q0, то есть S = q0,
- , если D(A, a) = B,

- , если D(A, a) = B и
 ,
,
- , если
 .
.
Доказательство того, что


В некоторых случаях для определения того, является ли язык регулярным, может быть полезным необходимое условие, которое называется леммой Огдена о разрастании.
Теорема 3.4. (Лемма о разрастании для регулярных множеств). Пусть L - регулярное множество. Существует такая константа k, что если

и




Доказательство. Пусть M = (Q, ?, D, q0, F) - конечный автомат, допускающий L, то есть L(M) = L и k = |Q|. Пусть



для некоторых






С помощью леммы о разрастании можно показать, что не является регулярным множеством язык L={0n1n|n

Допустим, что L регулярен. Тогда для достаточно большого n0n1n можно представить в виде xyz, причем y







