Теория и реализация языков программирования
Функции FIRST и FOLLOW
При построении таблицы предсказывающего анализатора нам потребуются две функции - FIRST и FOLLOW.
Пусть G = (N, T, P, S) - КС-грамматика. Для


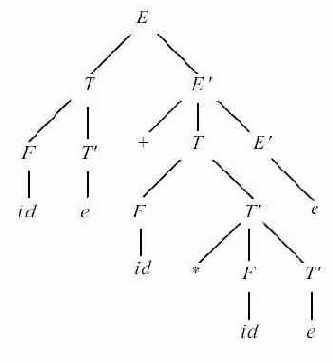
Рис. 4.3.
начинаются строки, выводимые из




Определим FOLLOW(A) для нетерминала A как множество терминалов a, которые могут появиться непосредственно справа от A в некоторой сентенциальной форме грамматики, то есть множество терминалов a таких, что существует вывод вида S



Рассмотрим алгоритмы вычисления функции FIRST.
Алгоритм 4.3. Вычисление FIRST для символов КС- грамматики.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FIRST(X) для каждого символа

Метод. Выполнить шаги 1-3:
(1) Если X - терминал, то положить FIRST(X) = {X}; если X - нетерминал, положить FIRST(X) =

(2) Если в P имеется правило X

(3) Пока ни к какому множеству FIRST(X) нельзя уже будет добавить новые элементы, выполнять:
do { continue = false; Для каждого нетерминала X Для каждого правила X


